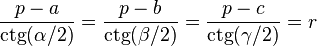Треуго́льник (в евклидовом пространстве) — геометрическая фигура, образованная тремя отрезками, которые соединяют три точки, не лежащие на одной прямой. Указанные три точки называются вершинами треугольника, а отрезки —сторонами треугольника. Стороны треугольника образуют в вершинах треугольника три угла. Другими словами, треугольник — это многоугольник, у которого имеется ровно три угла. Если три точки лежат на одной прямой, то «треугольник» с вершинами в трёх данных точках называется вырожденным. Все остальные треугольники невырожденные.
В неевклидовых пространствах в качестве сторон треугольника выступают геодезические линии, которые, как правило, являются криволинейными. Поэтому такие треугольники называют криволинейными. Важным частным случаем неевклидовых треугольников являются сферические треугольники.
Элементы треугольника
Треугольник с вершинами A, B и C обозначается как  (см. рис.). Треугольник
(см. рис.). Треугольник  имеет три стороны:
имеет три стороны:
 (см. рис.). Треугольник
(см. рис.). Треугольник  имеет три стороны:
имеет три стороны:- сторона
 ;
; - сторона
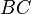 ;
; - сторона
 .
.
Длины сторон треугольника обозначаются строчными латинскими буквами (a, b, c):
 ;
; ;
;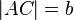 .
.
Треугольник  имеет следующие углы:
имеет следующие углы:
 имеет следующие углы:
имеет следующие углы:- угол
 — угол, образованный сторонами
— угол, образованный сторонами  и
и  и противолежащий стороне
и противолежащий стороне 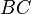 ;
; - угол
 — угол, образованный сторонами
— угол, образованный сторонами  и
и 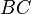 и противолежащий стороне
и противолежащий стороне  ;
; - угол
 — угол, образованный сторонами
— угол, образованный сторонами 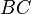 и
и  и противолежащий стороне
и противолежащий стороне  .
.
Величины углов при соответствующих вершинах традиционно обозначаются греческими буквами (α, β, γ).
- Внешним углом плоского треугольника при данной вершине называется угол, смежный внутреннему углу треугольника при этой вершине. Если внутренний угол при данной вершине треугольника образован двумя сторонами, выходящими из данной вершины, то внешний угол треугольника образован одной стороной, выходящей из данной вершины и продолжением другой стороны, выходящей из той же вершины.
Признаки равенства треугольников
Треугольник на евклидовой плоскости однозначно можно определить по следующим тройкам основных элементов:
- a, b, γ (равенство по двум сторонам и углу между ними);
- a, β, γ (равенство по стороне и двум прилежащим углам);
- a, b, c (равенство по трём сторонам).
Признаки равенства прямоугольных треугольников:
- по катету и гипотенузе;
- по двум катетам;
- по катету и острому углу;
- по гипотенузе и острому углу.
- по трём углам.
Типы треугольников
| Типы треугольников | ||
|---|---|---|
 Остроугольный |  Тупоугольный |  Прямоугольный |
 Разносторонний |  Равнобедренный | 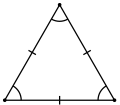 Равносторонний |
По величине углов
Поскольку в евклидовой геометрии сумма углов треугольника равна 180°, то не менее двух углов в треугольнике должны быть острыми(меньшими 90°). Выделяют следующие виды треугольников:
- Если все углы треугольника острые, то треугольник называется остроугольным;
- Если один из углов треугольника тупой (больше 90°), то треугольник называется тупоугольным;
- Если один из углов треугольника прямой (равен 90°), то треугольник называется прямоугольным. Две стороны, образующие прямой угол, называются катетами, а сторона, противолежащая прямому углу, называется гипотенузой.
В геометрии Лобачевского сумма углов треугольника всегда меньше 180°, а на сфере — всегда больше. Разность суммы углов треугольника и 180° называется дефектом. Дефект пропорционален площади треугольника, таким образом, у бесконечно малых треугольников на сфере или плоскости Лобачевского сумма углов будет мало отличаться от 180°.
По числу равных сторон
- Разносторонним (неравносторонним) называется треугольник, у которого все три стороны не равны.
- Равнобедренным называется треугольник, у которого две стороны равны. Эти стороны называются боковыми, третья сторона называется основанием. В равнобедренном треугольнике углы при основании равны. Высота,медиана и биссектриса равнобедренного треугольника, опущенные на основание, совпадают.
- Равносторонним или правильным называется треугольник, у которого все три стороны равны. В равностороннем треугольнике все углы равны 60°, а центры вписанной и описанной окружностей совпадают.
Лучи, отрезки и точки
- Медианой треугольника, проведённой из данной вершины, называется отрезок, соединяющий эту вершину с серединой противолежащей стороны (основанием медианы). Все три медианы треугольника пересекаются в одной точке. Эта точка пересечения называется центроидом или центром тяжести треугольника. Последнее название связано с тем, что у треугольника, сделанного из однородного материала, центр тяжести находится в точке пересечения медиан. Центроид делит каждую медиану в отношении 1:2, считая от основания медианы. Треугольник с вершинами в серединах медиан называется срединным треугольником.
- Основания медиан данного треугольника образуют так называемый дополнительный треугольник.
- Высотой треугольника, проведённой из данной вершины, называется перпендикуляр, опущенный из этой вершины на противоположную сторону или её продолжение. Три высоты треугольника пересекаются в одной точке, называемой ортоцентром треугольника. Треугольник с вершинами в основаниях высот называется ортотреугольником.
- Биссектрисой (биссéктором) треугольника, проведённой из данной вершины, называют отрезок, соединяющий эту вершину с точкой на противоположной стороне и делящий угол при данной вершине пополам. Биссектрисы треугольника пересекаются в одной точке, и эта точка совпадает с центром вписанной окружности (инцентром).
- Отрезок, соединяющий вершину с точкой на противоположной стороне, называется чевианой.
- Средней линией треугольника называют отрезок, соединяющий середины двух сторон этого треугольника. Три средние линии треугольника разделяют его на четыре равных треугольника в 4 раза меньшей площади, чем площадь исходного треугольника.
- Серединные перпендикуляры (медиатриссы) к сторонам треугольника также пересекаются в одной точке, которая совпадает с центром описанной окружности.
- В равнобедренном треугольнике медиана, высота и биссектриса, проведённые к основанию, совпадают. Верно и обратное: если биссектриса, медиана и высота, проведённые из одной вершины, совпадают, то треугольник равнобедренный.
- * Если треугольник разносторонний (неравносторонний), то внутренняя биссектриса, проведённая из любой его вершины, лежит между внутренними медианой и высотой, проведёнными из той же вершины.
- Чевианы, лежащие на прямых, изотомически сопряжённых биссектрисам относительно оснований медиан, называются антибиссектрисами. Они проходят через одну точку — центр антибиссектрис.
- Кливер треугольника — это отрезок, одна вершина которого находится в середине одной из сторон треугольника, вторая вершина находится на одной из двух оставшихся сторон, при этом кливер разбивает периметр пополам.
- Некоторые точки в треугольнике — «парные». Например, существует две точки, из которых все стороны видны либо под углом в 60°, либо под углом в 120°. Они называются точками Торричелли. Также существует две точки, проекции которых на стороны лежат в вершинах правильного треугольника. Это — точки Аполлония. Точки
 и
и  такие, что
такие, что  и
и  называются точками Брокара.
называются точками Брокара.
Окружности треугольника
Окружности, проходящие через вершины треугольника
- Описанная окружность (см. рис. справа) — окружность, проходящая через все три вершины треугольника. Описанная окружность всегда единственна, если треугольник не вырожден особым образом, то есть две из трех его вершин не совпадают.
- Окружность Джонсона — любая из трех окружностей (см. рис. справа), проходящая через две вершины треугольника и через его ортоцентр. Радиусы всех трех окружностей Джонсона равны. Окружности Джонсона являются описанными окружностями треугольников Гамильтона, имеющих в качестве двух вершин две вершины данного остроугольного треугольника, а в качестве третьей вершины имеющих его ортоцентр.
Окружности, касающиеся сторон треугольника или их продолжений
- Вписанная окружность (см. рис. справа) — окружность, касающаяся всех трёх сторон треугольника. Она единственна. Центр вписанной окружности называется инцентром.
- Отрезки, соединяющие точки касания вписанной окружности с вершинами, пересекаются в одной точке, называемой точкой Жергонна. Точка Жергонна изотомически сопряжена точке Нагеля
- Вневписанная окружность(см. рис. справа) — окружность, касающаяся одной стороны треугольника и продолжения двух других сторон. Таких окружностей в треугольнике три. Их радикальный центр — центр вписанной окружности срединного треугольника, называемый центром Шпикера или точкой Шпикера.
- Отрезки, соединяющие вершины с точками касания вневписанных окружностей с вершинами, пересекаются в одной точке, называемой точкой Нагеля.
Теорема о сумме углов треугольника
В невырожденном треугольнике сумма длин двух его сторон больше длины третьей стороны, в вырожденном — равна. Иначе говоря, длины сторон треугольника связаны следующими неравенствами:
 ;
; ;
;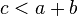 .
.
Неравенство треугольника является одной из аксиом метрики.
- Три положительных угла α, β и γ, каждый из которых меньше 180°, являются углами треугольника тогда и только тогда, когда выполняется любое одно из следующих соотношений:Тригонометрические тождества только с углами
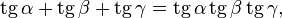 (первое тождество для тангенсов)
(первое тождество для тангенсов)
Замечание. Соотношение выше применимо только тогда, когда ни один из углов не равен 90° (в таком случае функция тангенса всегда определена).
(второе тождество для тангенсов)
 (первое тождество для синусов)
(первое тождество для синусов)
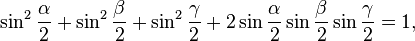 (второе тождество для синусов)
(второе тождество для синусов)
 (тождество для косинусов)
(тождество для косинусов)
Основные теоремы о треугольниках
Теорема синусов
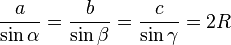 ,
,
где  — радиус окружности, описанной вокруг треугольника.
— радиус окружности, описанной вокруг треугольника.
 — радиус окружности, описанной вокруг треугольника.
— радиус окружности, описанной вокруг треугольника.
Из теоремы следует, что если  , то
, то  .
.
 , то
, то  .
.Теорема косинусов
Является обобщением теоремы Пифагора.
- Замечание. Теоремой косинусов также называют следующие две формулы, легко выводимые из основной теоремы косинусов (см. с. 51, ф. (1.11-2))
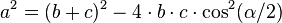 ,
,
 .
.
Теорема о проекциях
Теорема тангенсов
Теорема котангенсов
Прочие соотношения
Метрические соотношения в треугольнике приведены для  :
:
 :
:
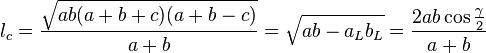
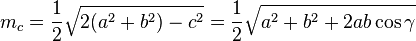

 — формула Эйлера
— формула Эйлера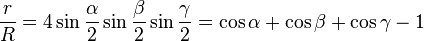

Где:
 ,
,  и
и  — стороны треугольника,
— стороны треугольника, — отрезки, на которые биссектриса
— отрезки, на которые биссектриса  делит сторону
делит сторону  ,
, — медианы, проведённые соответственно к сторонам
— медианы, проведённые соответственно к сторонам  ,
,  и
и  ,
, — высоты, опущенные соответственно на стороны
— высоты, опущенные соответственно на стороны  ,
,  и
и  ,
, — радиус вписанной окружности,
— радиус вписанной окружности, — радиус описанной окружности,
— радиус описанной окружности, — полупериметр,
— полупериметр, — площадь,
— площадь, — расстояние между центрами вписанной и описанной окружностей.
— расстояние между центрами вписанной и описанной окружностей.- Для любого треугольника, у которого стороны связаны неравенствами
 , а площадь равна
, а площадь равна  , длины срединных перпендикуляров или медиатрис, заключенных внутри треугольника, опущенных на соответствующую сторону (отмеченную нижним индексом), равны[30]:
, длины срединных перпендикуляров или медиатрис, заключенных внутри треугольника, опущенных на соответствующую сторону (отмеченную нижним индексом), равны[30]:

 and
and 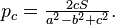
Радиусы вписанной и описанной окружностей
Следующие формулы включают радиусы описанной R и вписанной r окружностей:
где ha и т. д. высоты, проведенные к соответствующим сторонам;
и
 .
.
Произведение двух сторон треугольника равно произведению высоте к третьей стороне, умноженной на диаметр описаной окружности.
Площадь треугольника
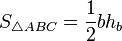 , так как
, так как  , то:
, то:

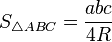
 — формула Герона
— формула Герона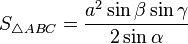


 ориентированная площадь треугольника.
ориентированная площадь треугольника. —
—
- Частные случаи
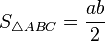 — для прямоугольного треугольника
— для прямоугольного треугольника — для равностороннего треугольника
— для равностороннего треугольника
- Обозначения
 — высота, проведённая на сторону
— высота, проведённая на сторону  ,
, — полупериметр,
— полупериметр, — радиус вписанной окружности,
— радиус вписанной окружности, — радиус вневписанной окружности, касающейся стороны
— радиус вневписанной окружности, касающейся стороны  ,
,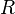 — радиус описанной окружности.
— радиус описанной окружности.
- Существуют другие формулы, такие, как например,
для угла α ≠ 90°.
- Обозначим через
 — радиус вписанной окружности, а через
— радиус вписанной окружности, а через  ,
,  и
и  — радиусы вневписанных окружностей, касающихся соответственно сторон
— радиусы вневписанных окружностей, касающихся соответственно сторон 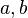 и
и  . Тогда имеем
. Тогда имеем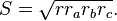
- В 1885, Бейкер (Baker) предложил список более ста формул площади треугольника. Он, в частности, включает:
![S = \frac{1}{2}[abch_ah_bh_c]^{1/3},](https://upload.wikimedia.org/math/5/d/2/5d2a4e4fd88ef1b1dc072b0d59a30920.png)


 .
.







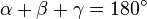

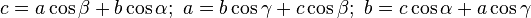
![\frac{a-b}{a+b} = \frac{\operatorname{tg}[\frac{1}{2}(\alpha-\beta)]}{\operatorname{tg}[\frac{1}{2}(\alpha+\beta)]}; \frac{b-c}{b+c} = \frac{\operatorname{tg}[\frac{1}{2}(\beta-\gamma)]}{\operatorname{tg}[\frac{1}{2}(\beta+\gamma)]}; \frac{a-c}{a+c} = \frac{\operatorname{tg}[\frac{1}{2}(\alpha-\gamma)]}{\operatorname{tg}[\frac{1}{2}(\alpha+\gamma)]}](https://upload.wikimedia.org/math/0/f/d/0fd52267dc784e837f5c54d21d122d34.png)